метричні задачі

1. Побудова взаємно перпендикулярних прямих, прямої і площини, площин
2. Визначення відстані між двома точками
3. Визначення відстані між точкою і прямою, між паралельними прямими
4. Визначення відстані між точкою і площиною, прямий і площиною, між площинами і перехресними прямими
5. Про проекціях плоских кутів
6. Визначення величини плоского кута по його ортогональних проекцій
7. Визначення кута між прямою і площиною
8. Визначення кута між площинами
9. Визначення кута між перехресними прямими

У § 6 гл. I зазначалося, що при паралельному, зокрема ортогональному, проектуванні геометричні фігури, довільно розташовані по відношенню до площин проекцій, проектуються на ці площини з спотворенням їх метричних характеристик (характеристик, які можуть бути отримані шляхом вимірювання лінійних і кутових величин). Для того щоб мати можливість по метрично спотвореним проекція судити про розміри і форму оригіналу, необхідно знати способи вирішення завдань щодо визначення неспотворених лінійних і кутових величин.

Метричними називаються завдання, вирішення яких пов'язане з перебуванням характеристик геометричних фігур, які визначаються (вимірюваних) лінійними і кутовими величинами.

Все різноманіття метричних задач, в кінцевому рахунку, зводиться до двох видів: А - завданням на визначення відстані між двома точками; Б - завданням на знаходження величини кута між двома пересічними прямими.

До метричних відносяться також завдання на побудову відрізка і кута з наперед заданим значенням відповідно лінійної і градусної (радіанної) величини.

Незважаючи на те, що чисто метричні задачі зустрічаються рідко, доцільно виделйть їх в самостійну групу, включивши в неї і ті завдання, в яких на проміжних етапах рішення доводиться з'ясовувати позиційні відносини між геометричними фігурами.

В основі алгоритму розв'язання будь-якої метричної задачі лежить інваріантне властивість ортогонального проектування, що полягає в тому, що будь-яка фігура, що належить площині, паралельній площині проекції, проектується на цю площину в конгруентність фігуру, т. Е. (Ф ⊂ β) ∧ (β || π1) ⇒ Ф '≅ Ф.

Розглянемо можливі шляхи вирішення завдань на визначення метричних характеристик геометричних фігур.

А. Визначення відстаней.

Рішення задач на визначення відстані між точкою і прямою, двома паралельними прямими, точкою і площиною, прямий і площиною, двома площинами, перехресними прямими, в кінцевому рахунку, зводиться до знаходження відстані між двома точками.

Креслення на рис. 248 підтверджують це твердження. З цих креслень видно також, що, перш ніж приступити до вирішення завдання на визначення відстані між точкою і прямою або двома паралельними прямими (рис. 248, а і б), необхідно провести площину γ, перпендикулярну до прямої l, або опустити перпендикуляр з точки А (A ∈ m або A ∈ β) на площину α (рис. 248, в, г, д, е). Тому, перш ніж вирішувати завдання на визначення відстаней, з'ясуємо характер і последо-

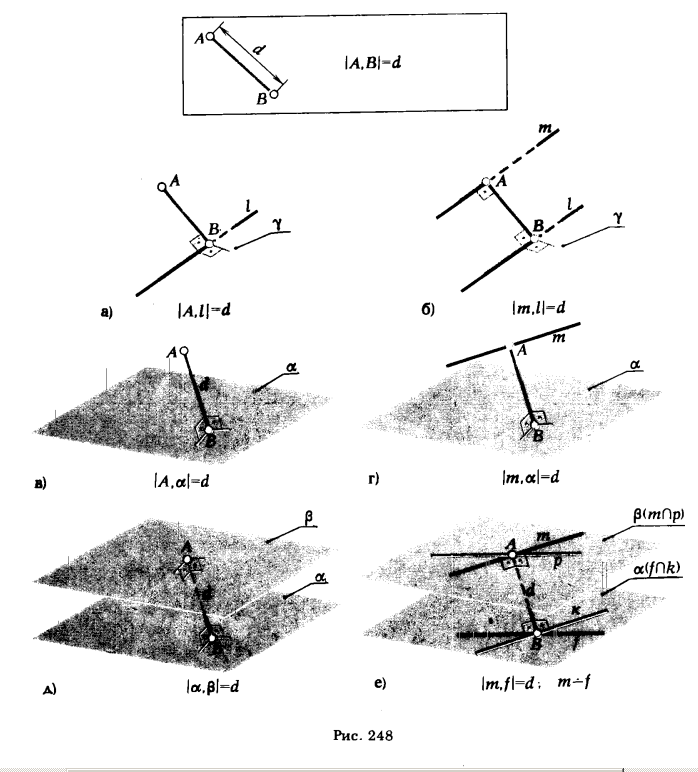
вательность графічних побудов, які повинні бути виконані для побудови на епюрі взаємно перпендикулярних прямих, прямої і площини, площин.

• Побудова взаємно перпендикулярних прямих, прямої і площини, площин

  Не буде перебільшенням стверджувати, що побудова взаємно перпендикулярних прямих і площин поряд з визначенням відстані між двома точками є основними графічними операціями при вирішенні метричних задач. Детальніше

• Визначення відстані між двома точками

  У § 8 гл. I (див. Рис. 50) було показано графічне визначення довжини відрізка [АВ], що є мірою відстані між точками А і В, шляхом побудови прямокутного трикутника. Детальніше

• Визначення відстані між точкою і прямою, між паралельними прямими

  Відстань від точки до прямої визначається довжиною відрізка перпендикуляра, опущеного з точки на пряму. Детальніше

• Визначення відстані між точкою і площиною, прямий і площиною, між площинами і перехресними прямими

  Визначення відстані між: 1 - точкою і площиною; 2 - прямий і площиною; 3 - площинами; 4 - перехресними прямими розглядається спільно, так як алгоритм рішення для всіх цих завдань по суті однаковий і складається з геометричних побудов, які потрібно виконати для визначення відстані між заданими точкою А і площиною α. Детальніше

• Про проекціях плоских кутів

  Відзначимо ряд властивостей ортогональних проекцій плоских кутів, знання яких допоможе в подальшому правильно читати епюр і вирішувати завдання по визначенню величини кута, якщо відомі його ортогональні проекції. Детальніше

• Визначення величини плоского кута по його ортогональних проекцій

  У попередньому параграфі було відзначено, що плоский кут проектується на площину проекції без спотворення в тому випадку, коли його сторони паралельні цій площині. Ця властивість може бути прийнято за основу при складанні алгоритму розв'язання задачі на визначення величини кута по його спотвореним ортогональним проекція. Детальніше

• Визначення кута між прямою і площиною

  Визначення кута між прямою і площиною, двома площинами, перехресними прямими, зводиться до знаходження кута між двома прямими. Детальніше

• Визначення кута між площинами

  Мірою кута між двома площинами служить лінійний кут, утворений двома прямими - перетинами граней цього кута площиною, перпендикулярної до їх ребру. Детальніше

• Визначення кута між перехресними прямими

  Кутом між перехресними прямими називається плоский кут, який утворюється між прямими, проведеними з довільної точки простору паралельно даними перехресних прямих. Детальніше